Richter magnitude scale
| Part of a series on earthquakes |
|---|
| Types |
| Foreshock • Aftershock • Blind thrust Doublet • Interplate • Intraplate Megathrust • Remotely triggered • Slow Submarine • Supershear Tsunami • Earthquake swarm |
| Causes |
| Fault movement • Volcanism • Induced seismicity |
| Characteristics |
| Epicenter • Hypocenter • Shadow zone Seismic wave • P-wave • S-wave |
| Measurement |
| Mercalli scale • Richter scale Moment scale • Surface wave magnitude scale Body wave magnitude scale • Seismometer Earthquake duration magnitude |
| Prediction |
| Coordinating Committee for Earthquake Prediction Earthquake sensitive |
| Other |
| Shear wave splitting • Adams–Williamson equation Flinn-Engdahl regions • Earthquake engineering Seismite • Seismology |
The expression Richter magnitude scale refers to a number of ways to assign a single number to quantify the energy contained in an earthquake.
In all cases, the magnitude is a base-10 logarithmic scale obtained by calculating the logarithm of the amplitude of waves measured by a seismograph. An earthquake that measures 5.0 on the Richter scale has a shaking amplitude 10 times larger and corresponds to an energy release of √1000 ≈ 31.6 times greater than one that measures 4.0.[1]
Contents |
Development
Developed in 1935 by Charles Richter in partnership with Beno Gutenberg, both of the California Institute of Technology, the scale was firstly intended to be used only in a particular study area in California, and on seismograms recorded on a particular instrument, the Wood-Anderson torsion seismograph. Richter originally reported values to the nearest quarter of a unit, but values were later reported with one decimal place. His motivation for creating the local magnitude scale was to compare the size of different earthquakes.[1]
His inspiration was the apparent magnitude scale used in astronomy to describe the brightness of stars and other celestial objects.[2] Richter arbitrarily chose a magnitude 0 event to be an earthquake that would show a maximum combined horizontal displacement of 1 µm (0.00004 in) on a seismogram recorded using a Wood-Anderson torsion seismograph 100 km (62 mi) from the earthquake epicenter. This choice was intended to prevent negative magnitudes from being assigned. The smallest earthquakes that could be recorded and located at the time were of magnitude 3, approximately. However, the Richter scale has no lower limit, and sensitive modern seismographs now routinely record quakes with negative magnitudes.
ML (local magnitude) was not designed to be applied to data with distances to the hypocenter of the earthquake greater than 600 km[3] (373 mi). For national and local seismological observatories the standard magnitude scale is today still ML. Unfortunately this scale saturates at M6.5, approximately, because the high frequency waves recorded locally have wavelengths shorter than the rupture lengths of large earthquakes.
To be able to measure the size of earthquakes around the globe, Gutenberg and Richter later developed a magnitude scale based on surface waves, surface wave magnitude MS; and another based on body waves, body wave magnitude mb.[4] These are types of waves that are recorded at teleseismic distances. The two scales were adjusted such that they were consistent with the ML scale. This succeeded better with the Ms scale than with the mb scale. Both of these scales saturate when the earthquake is bigger than magnitude 8 and therefore the moment magnitude scale, Mw, was invented.[5]
These older magnitude scales have been superseded by the implementation of methods for estimating the seismic moment, creating the moment magnitude scale, although the former are still widely used because they can be calculated quickly.
Details
The Richter scale proper was defined in 1935 for particular circumstances and instruments; the instrument used saturated for strong earthquakes. The scale was replaced by the moment magnitude scale (MMS); for earthquakes adequately measured by the Richter scale, numerical values are approximately the same. Although values measured for earthquakes now are actually 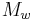 (MMS), they are frequently reported as Richter values, even for earthquakes of magnitude over 8, where the Richter scale becomes meaningless. Anything above 5 is classed as a risk.
(MMS), they are frequently reported as Richter values, even for earthquakes of magnitude over 8, where the Richter scale becomes meaningless. Anything above 5 is classed as a risk.
The Richter and MMS scales measure the energy released by an earthquake; another scale, the Mercalli intensity scale, classifies earthquakes by their effects, from detectable by instruments but not noticeable to catastrophic. The energy and effects are not necessarily strongly correlated; a shallow earthquake in a populated area with soil of certain types can be far more intense than a much more energetic deep earthquake in an isolated area.
There are several scales which have historically been described as the "Richter scale," especially the local magnitude 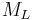 and the surface wave
and the surface wave 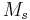 scale. In addition, the body wave magnitude,
scale. In addition, the body wave magnitude, 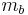 , and the moment magnitude,
, and the moment magnitude, 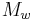 , abbreviated MMS, have been widely used for decades, and a couple of new techniques to measure magnitude are in the development stage.
, abbreviated MMS, have been widely used for decades, and a couple of new techniques to measure magnitude are in the development stage.
All magnitude scales have been designed to give numerically similar results. This goal has been achieved well for 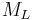 ,
, 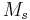 , and
, and 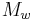 .[6][7] The
.[6][7] The 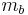 scale gives somewhat different values than the other scales. The reason for so many different ways to measure the same thing is that at different distances, for different hypocentral depths, and for different earthquake sizes, the amplitudes of different types of elastic waves must be measured.
scale gives somewhat different values than the other scales. The reason for so many different ways to measure the same thing is that at different distances, for different hypocentral depths, and for different earthquake sizes, the amplitudes of different types of elastic waves must be measured.
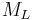 is the scale used for the majority of earthquakes reported (tens of thousands) by local and regional seismological observatories. For large earthquakes worldwide, the moment magnitude scale is most common, although
is the scale used for the majority of earthquakes reported (tens of thousands) by local and regional seismological observatories. For large earthquakes worldwide, the moment magnitude scale is most common, although 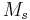 is also reported frequently.
is also reported frequently.
The seismic moment, 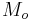 , is proportional to the area of the rupture times the average slip that took place in the earthquake, thus it measures the physical size of the event.
, is proportional to the area of the rupture times the average slip that took place in the earthquake, thus it measures the physical size of the event. 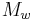 is derived from it empirically as a quantity without units, just a number designed to conform to the
is derived from it empirically as a quantity without units, just a number designed to conform to the 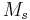 scale.[8] A spectral analysis is required to obtain
scale.[8] A spectral analysis is required to obtain 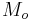 , whereas the other magnitudes are derived from a simple measurement of the amplitude of a specifically defined wave.
, whereas the other magnitudes are derived from a simple measurement of the amplitude of a specifically defined wave.
All scales, except 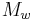 , saturate for large earthquakes, meaning they are based on the amplitudes of waves which have a wavelength shorter than the rupture length of the earthquakes. These short waves (high frequency waves) are too short a yardstick to measure the extent of the event. The resulting effective upper limit of measurement for
, saturate for large earthquakes, meaning they are based on the amplitudes of waves which have a wavelength shorter than the rupture length of the earthquakes. These short waves (high frequency waves) are too short a yardstick to measure the extent of the event. The resulting effective upper limit of measurement for 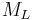 is about 6.5 and about 8 for
is about 6.5 and about 8 for 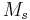 .[9]
.[9]
New techniques to avoid the saturation problem and to measure magnitudes rapidly for very large earthquakes are being developed. One of these is based on the long period P-wave,[10] the other is based on a recently discovered channel wave.[11]
The energy release of an earthquake, which closely correlates to its destructive power, scales with the 3⁄2 power of the shaking amplitude. Thus, a difference in magnitude of 1.0 is equivalent to a factor of 31.6 (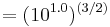 ) in the energy released; a difference in magnitude of 2.0 is equivalent to a factor of 1000 (
) in the energy released; a difference in magnitude of 2.0 is equivalent to a factor of 1000 (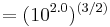 ) in the energy released.[12] The elastic energy radiated is best derived from an integration of the radiated spectrum, but one can base an estimate on
) in the energy released.[12] The elastic energy radiated is best derived from an integration of the radiated spectrum, but one can base an estimate on 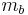 because most energy is carried by the high frequency waves.
because most energy is carried by the high frequency waves.
Richter magnitudes
The Richter magnitude of an earthquake is determined from the logarithm of the amplitude of waves recorded by seismographs (adjustments are included to compensate for the variation in the distance between the various seismographs and the epicenter of the earthquake). The original formula is:[13]
where A is the maximum excursion of the Wood-Anderson seismograph, the empirical function A0 depends only on the epicentral distance of the station,  . In practice, readings from all observing stations are averaged after adjustment with station-specific corrections to obtain the ML value.
. In practice, readings from all observing stations are averaged after adjustment with station-specific corrections to obtain the ML value.
Because of the logarithmic basis of the scale, each whole number increase in magnitude represents a tenfold increase in measured amplitude; in terms of energy, each whole number increase corresponds to an increase of about 31.6 times the amount of energy released, and each increase of 0.2 corresponds to a doubling of the energy released.
Events with magnitudes greater than about 4.6 are strong enough to be recorded by a seismograph anywhere in the world, so long as its sensors are not located in the earthquake's shadow.
The following describes the typical effects of earthquakes of various magnitudes near the epicenter. The values are typical only and should be taken with extreme caution, since intensity and thus ground effects depend not only on the magnitude, but also on the distance to the epicenter, the depth of the earthquake's focus beneath the epicenter, and geological conditions (certain terrains can amplify seismic signals).
| Magnitude | Description | Earthquake effects | Frequency of occurrence |
|---|---|---|---|
| Less than 2.0 | Micro | Micro earthquakes, not felt.[14] | Continual |
| 2.0–2.9 | Minor | Generally not felt, but recorded. | 1,300,000 per year (est.) |
| 3.0–3.9 | Often felt, but rarely causes damage. | 130,000 per year (est.) | |
| 4.0–4.9 | Light | Noticeable shaking of indoor items, rattling noises. Significant damage unlikely. | 13,000 per year (est.) |
| 5.0–5.9 | Moderate | Can cause major damage to poorly constructed buildings over small regions. At most slight damage to well-designed buildings. | 1,319 per year |
| 6.0–6.9 | Strong | Can be destructive in areas up to about 160 kilometres (99 mi) across in populated areas. | 134 per year |
| 7.0–7.9 | Major | Can cause serious damage over larger areas. | 15 per year |
| 8.0–8.9 | Great | Can cause serious damage in areas several hundred kilometres across. | 1 per year |
| 9.0–9.9 | Devastating in areas several thousand kilometres across. |
1 per 10 years (est.) | |
| 10.0+ | Massive | Never recorded, widespread devastation across very large areas; see below for equivalent seismic energy yield. |
Extremely rare (Unknown/May not be possible) |
(Based on U.S. Geological Survey documents.)[15]
Great earthquakes occur once a year, on average. The largest recorded earthquake was the Great Chilean Earthquake of May 22, 1960, which had a magnitude of 9.5 on the moment magnitude scale.[16] The Richter scale is open ended. There is no upper limit to the magnitude of an earthquake on the Richter scale.[17]
Examples
The following table lists the approximate energy equivalents in terms of TNT explosive force – though note that the earthquake energy is released underground rather than overground.[18] Most energy from an earthquake is not transmitted to and through the surface; instead, it dissipates into the crust and other subsurface structures. In contrast, a small atomic bomb blast (see nuclear weapon yield) will not simply cause light shaking of indoor items, since its energy is released above ground.
Following, 31.623 to the power of 0 equals 1, 31.623 to the power of 1 equals 31.623 and 31.623 to the power of 2 equals 1000. Therefore, an 8.0 on the Richter scale releases 31.623 times more energy than a 7.0 and a 9.0 on the Richter scale releases 1000 times more energy than a 7.0.
- Quakes using the more modern magnitude scales will denote their abbreviations:
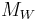 and
and 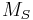 . Those that have no denoted prefix are
. Those that have no denoted prefix are 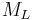 . Please be advised that the magnitude "number" (example 7.0) displayed for those quakes on this table may represent a significantly greater or lesser release in energy than by the correctly given magnitude (example
. Please be advised that the magnitude "number" (example 7.0) displayed for those quakes on this table may represent a significantly greater or lesser release in energy than by the correctly given magnitude (example 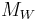 ).
).
See also
- Earthquake
- Largest earthquakes by magnitude
- Seismic scale
- Seismite
- Mercalli intensity scale
- Moment magnitude scale
- Japan Meteorological Agency seismic intensity scale
- Order of magnitude
- Rohn Emergency Scale for measuring the magnitude (intensity) of any emergency
References
- ^ a b The Richter Magnitude Scale
- ^ Hough, S.E. (2007). Richter's scale: measure of an earthquake, measure of a man. Princeton University Press. p. 121. ISBN 9780691128078. http://books.google.co.uk/books?id=rvmDeAxEiO8C&pg=PA121&dq=richter+scale+star+brightness&hl=en&ei=bA7jToe6M4Wc8gOPgJH5Aw&sa=X&oi=book_result&ct=result&resnum=1&sqi=2&ved=0CDQQ6AEwAA#v=onepage&q=richter%20scale%20star%20brightness&f=false. Retrieved 10 December 2011.
- ^ "USGS Earthquake Magnitude Policy". USGS. March 29, 2010. http://earthquake.usgs.gov/aboutus/docs/020204mag_policy.php.
- ^ William L. Ellsworth (1991). SURFACE-WAVE MAGNITUDE (Ms) AND BODY-WAVE MAGNITUDE (mb). USGS. http://www.johnmartin.com/earthquakes/eqsafs/safs_694.htm. Retrieved 2008-09-14.
- ^ Kanamori
- ^ Richter, C.F., 1936. "An instrumental earthquake magnitude scale", Bulletin of the Seismological Society of America 25, no., 1-32.
- ^ Richter, C.F., "Elementary Seismology", edn, Vol., W. H. Freeman and Co., San Francisco, 1956.
- ^ Hanks, T. C. and H. Kanamori, 1979, "Moment magnitude scale", Journal of Geophysical Research, 84, B5, 2348.
- ^ "Richter scale". Glossary. USGS. March 31, 2010. http://earthquake.usgs.gov/hazards/qfaults/glossary.php.
- ^ Di Giacomo, D., Parolai, S., Saul, J., Grosser, H., Bormann, P., Wang, R. & Zschau, J., 2008. Rapid determination of the enrgy magnitude Me, in European Seismological Commission 31st General Assembly, Hersonissos.
- ^ Rivera, L. & Kanamori, H., 2008. Rapid source inversion of W phase for tsunami warning, in European Geophysical Union General Assembly, pp. A-06228, Vienna.
- ^ USGS: Measuring the Size of an Earthquake, Section 'Energy, E'
- ^ Ellsworth, William L. (1991). The Richter Scale ML, from The San Andreas Fault System, California (Professional Paper 1515). USGS. pp. c6, p177. http://www.johnmartin.com/earthquakes/eqsafs/safs_693.htm. Retrieved 2008-09-14.
- ^ This is what Richter wrote in his Elementary Seismology (1958), an opinion copiously reproduced afterwards in Earth's science primers. Recent evidence shows that earthquakes with negative magnitudes (down to −0.7) can also be felt in exceptional cases, especially when the focus is very shallow (a few hundred metres). See: Thouvenot, F.; Bouchon, M. (2008). What is the lowest magnitude threshold at which an earthquake can be felt or heard, or objects thrown into the air?, in Fréchet, J., Meghraoui, M. & Stucchi, M. (eds), Modern Approaches in Solid Earth Sciences (vol. 2), Historical Seismology: Interdisciplinary Studies of Past and Recent Earthquakes, Springer, Dordrecht, 313–326.
- ^ [1]
- ^ USGS: List of World's Largest Earthquakes
- ^ http://tremor.nmt.edu/faq/how.html
- ^ FAQs – Measuring Earthquakes
- ^ "Magnitude 5.0 – Ontario-Quebec border region, Canada". earthquake.usgs.gov. http://earthquake.usgs.gov/earthquakes/recenteqsww/Quakes/us2010xwa7.php#details. Retrieved 2010-06-23.
- ^ "Moderate 5.0 earthquake shakes Toronto, Eastern Canada and U.S.". nationalpost.com. http://news.nationalpost.com/2010/06/23/tremors-felt-in-toronto-ottawa-reports/. Retrieved 2010-06-23.
- ^ km al NOROESTE de ZUMPANGO DEL RIO, GRO ®resar=catalogo1 "Zumpango Del Rio Earthquake" (in Mexican). Servicio Sismologico Nacional. http://www.ssn.unam.mx/website/jsp/localizacion.jsp?&archivo=111210_194725.gif&evento=1&fecha=2011-12-10&hora=19:47:25&latitud=17.84&longitud=-99.98&profundidad=58&magnitud=6.5&epicentro=53 km al NOROESTE de ZUMPANGO DEL RIO, GRO ®resar=catalogo1. Retrieved 28 December 2011.
- ^ "M8.1 South End of Island August 8, 1993.". eeri.org. http://www.eeri.org/site/reconnaissance-activities/64-guam/182-m81southendofisland. Retrieved 2011-03-11..
- ^ Petraglia, M.; R. Korisettar, N. Boivin, C. Clarkson,4 P. Ditchfield,5 S. Jones,6 J. Koshy,7 M.M. Lahr,8 C. Oppenheimer,9 D. Pyle,10 R. Roberts,11 J.-C. Schwenninger,12 L. Arnold,13 K. White. (6 July 2007). "Middle Paleolithic Assemblages from the Indian Subcontinent Before and After the Toba Super-eruption". Science 317 (5834): 114–116. doi:10.1126/science.1141564. PMID 17615356.
- ^ Bralower, Timothy J.; Charles K. Paull; R. Mark Leckie (1998). "The Cretaceous-Tertiary boundary cocktail: Chicxulub impact triggers margin collapse and extensive sediment gravity flows". Geology 26: 331–334. Bibcode 1998Geo....26..331B. doi:10.1130/0091-7613(1998)026<0331:TCTBCC>2.3.CO;2. ISSN 0091-7613. http://www.geosc.psu.edu/people/faculty/personalpages/tbralower/Braloweretal1998.pdf. Retrieved 2009-09-03.
- ^ Klaus, Adam; Norris, Richard D.; Kroon, Dick; Smit, Jan (2000). "Impact-induced mass wasting at the K-T boundary: Blake Nose, western North Atlantic". Geology 28: 319–322. Bibcode 2000Geo....28..319K. doi:10.1130/0091-7613(2000)28<319:IMWATK>2.0.CO;2. ISSN 0091-7613.
- ^ Busby, Cathy J.; Grant Yip; Lars Blikra; Paul Renne (2002). "Coastal landsliding and catastrophic sedimentation triggered by Cretaceous-Tertiary bolide impact: A Pacific margin example?". Geology 30: 687–690. Bibcode 2002Geo....30..687B. doi:10.1130/0091-7613(2002)030<0687:CLACST>2.0.CO;2. ISSN 0091-7613.
- ^ Simms, Michael J. (2003). "Uniquely extensive seismite from the latest Triassic of the United Kingdom: Evidence for bolide impact?". Geology 31: 557–560. Bibcode 2003Geo....31..557S. doi:10.1130/0091-7613(2003)031<0557:UESFTL>2.0.CO;2. ISSN 0091-7613.
- ^ Simkin, Tom; Robert I. Tilling; Peter R. Vogt; Stephen H. Kirby; Paul Kimberly; David B. Stewart (2006). "This dynamic planet. World map of volcanoes, earthquakes, impact craters, and plate tectonics. Inset VI. Impacting extraterrestrials scar planetary surfaces". U.S. Geological Survey. http://mineralsciences.si.edu/tdpmap/pdfs/impact.pdf. Retrieved 2009-09-03.
- ^ Phil Plait (2009). "Anniversary of a cosmic blast". discovermagazine.com. http://blogs.discovermagazine.com/badastronomy/2009/12/27/anniversary-of-a-cosmic-blast/. Retrieved 2010-11-26.
External links
- IRIS Real-time Seismic Monitor of the Earth
- USGS: magnitude and intensity comparison
- USGS: Earthquake Magnitude Policy
- USGS: 2000–2006 Earthquakes worldwide
- USGS: 1990–1999 Earthquakes worldwide
- Alaska Railroad Earthquake with a table of yield-to-magnitude relations.
|
|||||||||||||
![M_\mathrm{L} = \log_{10} A - \log_{10} A_\mathrm{0}(\delta) = \log_{10} [A / A_\mathrm{0}(\delta)],\](/2012-wikipedia_en_all_nopic_01_2012/I/13e5e0759d863fbb88d35d2ca1421b7b.png)